fellowhuman

Here are my notes on the 2015 CMC-North conference, plus a little neat graphical stuff (and doodles of the rooms some of the talks were held in).

Friday Keynote: Practices for discussion

By Matt Larson. I took this largely as a pep talk about the current state of math education and our challenges in communicating our process and intention to parents; much of it was directed at issues that (thankfully) I don’t often have to deal with in my school’s culture. However, it also introduced me to the NCTM Principles to Actions document, whose most useful feature for me (as far as I can tell) is a set of “Mathematics Teaching Practices”:

• Establish mathematics goals
• Implement tasks that promote reasoning and problem solving
• Use and connect representations
• Facilitate meaningful mathematical discourse
• Pose purposeful questions
• Build procedural fluency from conceptual understanding
• Support productive struggle
• Elicit and use evidence of student thinking

Some other points were good reminders:

• Tracking is an obstacle to equity.
• A school’s best teachers should be assigned to its lowest-level classes.
• We (U.S. teachers) spend too little time planning lessons — cf. Chinese practice of putting many hours in to prep one 45-minute lesson — and should collaboratively plan one lesson per unit to counter this habit.
• Co-planning of lessons correlates strongly with better learning outcomes.
• Ask questions that make students struggle; then, avoid the temptation to jump in and rescue them when they express frustration.

Two book pointers: Words that Work and 5 Practices for Orchestrating Productive Mathematics Discussions. We should get a department copy of that second book, I think!

Jessica Balli: Perseverance in exploration

This talk introduced Bongard problems as a tool for teaching mathematical thinking. Named after a Russian AI researcher (who published a book of them), each of these is two sets of six images; the problem is to determine a rule that includes all of one set and excludes all of the other.

Example uses of them:

• warm-up at beginning of class, with each student writing a rule and then sharing
• show first two images of each set, and share rules; then show second two, and revise rules; then show third pair, and revise rules. (She presented a template she’d devised for stating & revising rules.)

Importantly, it’s all about the discourse around the puzzles: getting all the rules out into the open, examining different correct (and incorrect) ways of stating a rule, critiquing rules, suggesting improvements to rules, and so on.

Anna Blinstein: Writing in math

I have students do a lot of journaling already, so I was curious how someone else does it. Main points:

• Decide whether you’re having students write for learning & assessment, or for metacognition, SEL, and rapport-building. This informs your choice of prompts.
• It’s helpful to ask (in journal prompts) about non-math happenings in your students’ lives too. There’s a lot you can learn that will usefully inform your teaching.

Julie Yu: The math of mirrors

Good presenter!

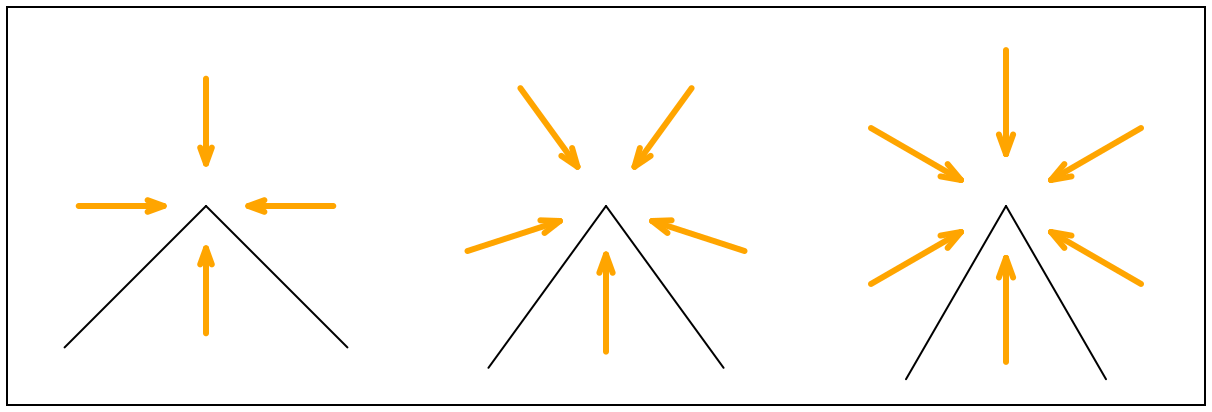
The warm-up was an exercise in which each of us taped together two small rectangular acrylic mirrors so they were hinged on one side. Julie had prepared a sheet that included angles looking like this:

The prompt was, “For each picture, predict how many arrows you will see if you place the mirrors on the two sides of the angle.”

Then we could confirm using the mirrors, producing results like this:

There was a second sheet that worked similarly, but with more interesting patterns:

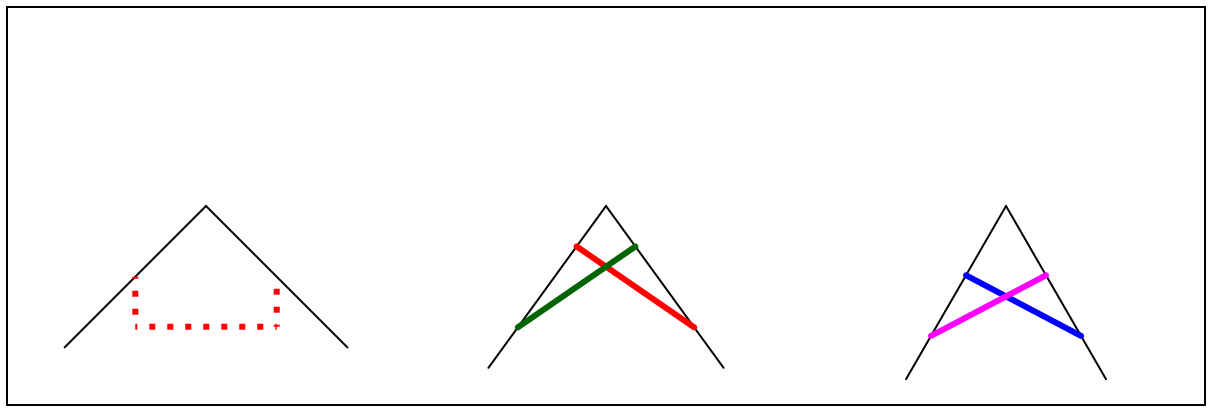
We were invited to sketch what we expected to see — more challenging than it looked at first! — and, again, check with the mirrors:

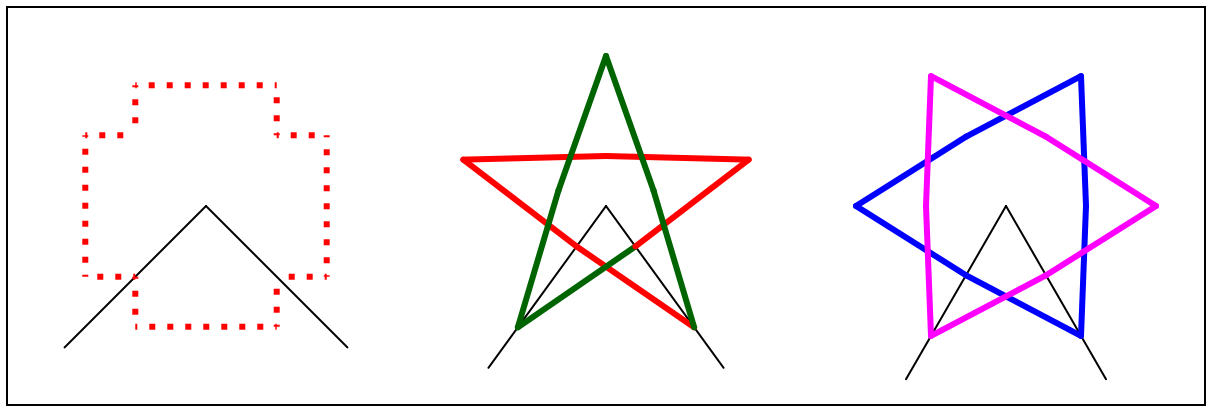
The rest of this presentation went towards exploring the question, “How large does a mirror need to be for you to see your whole body in it, without wasted space above, below, or on either side?” This is a fun problem, already familiar to me from Harold Jacobs’ excellent geometry book. We’ll assume this is a wall-mounted mirror, and therefore that the mirror is perpendicular to the ground (and parallel to you, the viewer).

Warning: spoilers ahead. If you want to solve the problem, come back to this post later.

So, Julie had a volunteer stand in front of a full-length wall mirror, at a length equal to the volunteer’s height, h — which became our unit of measure. On the mirror, we taped a rectangular border around the portion of the mirror necessary for our volunteer to see herself. So, the situation looked like this:

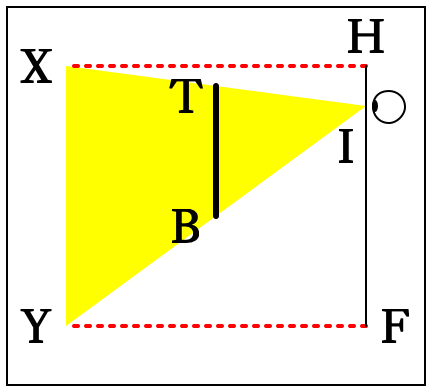
Our volunteer is HF, looking at the mirror TB, seeing her reflection XY. Her eye level is at point I.

At this point in the session, a lot of folks were surprised at just how small the necessary rectangle of mirror really was.

Next question: If she stands twice as far from the mirror, will we need our mirror to be smaller, larger, or the same size? Here’s a diagram:

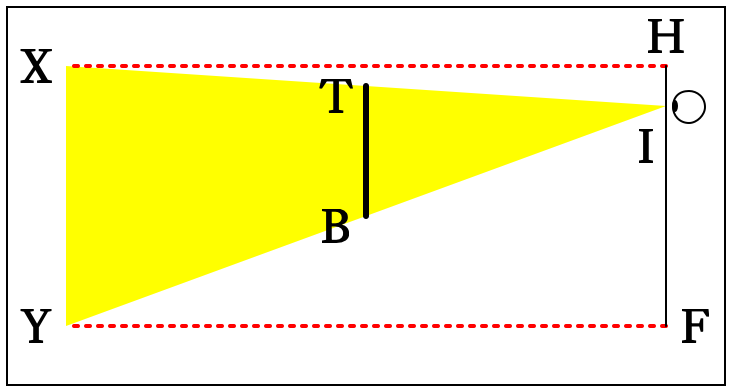
And the answer is...the same size! So, to all appearances, the mirror length is independent of the viewer’s distance from the mirror. I’ll leave the proof as an exercise; the most obvious method (to me, at least) involves similar triangles.

The session concluded with a look at cylindrical and conical mirrors — simple mylar sheets wrapped around soda cans, or taped into cone shape — and a fun exercise in which we placed beans around a cylinder to make their reflection appear as a straight line.

Andrew Stadel: Mistake analysis

Actually, what was most memorable to me about this talk was the use of clotheslines as number lines, and in particular, the idea of running two clotheslines in parallel as a dynamic representation of an equation. He’s summarized this well on his blog, so I won’t retread it here.

Also — and since I’m basing this on my notes, some fifteen days later, I’m probably deviating from what he said — he offered one form of activity for recurring use: presenting wrong answers and asking the students to discuss what thinking led to them and where the misconceptions lie. For example, we discussed some exponential mix-ups he offered:

• \(2^5 = 10\)
• \((-2)^3 = 8\)
• \(-6^2 = 36\)
• \(37^0 = 0\)
• \(100^{1/2} = 50\)
• \(7^{-2} = -49\)
• \((y^3)^5 = y^8\)
• \(\frac{x^5}{x^9} = x^4\)

Lew Douglas & Henri Picciotto: Transformations

This session discussed how to organize a coherent geometry curriculum around transformations, with side tracks into using 1-D translation, reflection, and dilation to study integer arithmetic (on the number line) and using rotation to study complex numbers. The main thesis was (roughly) that a transformational approach can eliminate some of the pedantic details common to traditional geometry, and lead to a more logical, consistent, and unified curriculum.

The geometry discussion included axioms for construction...

1. Two lines intersect in at most one point.
2. A circle and a line intersect in at most two points.
3. Two circles intersect in at most two points.

...and one transformation axiom, reflection preserves distance and angle measure. The speakers also walked through some transformation-based proofs of statements such as:

• For all points P and Q, there exists a reflection mapping P to Q.
• A point P is equidistant from points A and B iff it lies on the perpendicular bisector of AB.
• The SSS congruence theorem.

I was mildly bugged by their defining rotation and translation in terms of reflection — I’ve done that in the past, but I’m uneasy about it because it replaces a meaning-based definition with a mathematically opportunistic one that’s less meaningful. If we define rotation and translation more meaningfully, it’s easier to extract facts from the definitions. For example, this is how I’d define rotation:

• Rotating a point \(P\) around a point \(C\) by angle \(x\) produces a point \(P’\), with \(PC = P’C\) and \(\angle PCP’ = x\).
• A rotation is a transformation that rotates every point by the same angle about the same center.

From this definition we can prove that a rotation is equivalent to two reflections through intersecting lines — which to me is a beautifully interesting mathematical fact that’s incidental to the definition, not central to the nature of reflection. (Also, it serves as another illustration of bootstrapping a complex definition by defining an operation on a point and then “lifting” that operation to the plane.)

I do think comparing the above definition of rotation with the one that uses reflection is a great discussion to have with students, however; we often fail to devote much time to comparing pros and cons of definitions, but students need to learn that mathematical definitions aren’t chosen by fiat, and such comparisons are one way to get that point across.

Also worth noting: focusing on transformation opens different avenues for proving basic facts (such as “Vertical angles are equal”), and at least for the examples they showed, the proofs look possibly simpler to me. I see a connection to the imperative/declarative dichotomy in programming. After thinking about that distinction (and the controversy around it in CS0/CS1 courses) for years, I’ve concluded that

• simple tasks are easier to explain crudely in imperative terms
• complex tasks are vastly easier to understand declaratively
• declarative thinking, along with the language of definitions, is a major stumbling block for many math and CS students — who must push through it in order to become clear thinkers

Here, transformations may let us cast the geometric and algebraic ideas in imperative terms that the students are more intuitively comfortable with, and it’s quite possible to drill down to axioms and equations to get rigorous proofs that challenge students to think declaratively.

Sunday Keynotes

Grace Kelemanik on the SMPs

This speaker discussed using the eight Standards for Mathematical Practice — particularly, how eight is too many to think about on a daily basis, and how to use them to manageably guide instruction. Her strategy is to focus on SMPs #2 (re quantitative thinking), #7 (re structural thinking), and #8 (re looking for repeated reasoning):

• Quantitative reasoning focuses on identifying quantities and relationships in the problem.
• Structural reasoning focuses on identifying and grouping meaningful chunks of structure within the problem; changing elements of the problem into a more convenient form; and connecting problem elements to familiar structures. Slogan: Chunk, change, connect.
• Looking for repeated reasoning is not about number patterns; it is about finding repetition in the processes you use in the problem — typically, processes like counting, calculating, or constructing. Often identified by phrases like “Every time, I...” or “It always...” or “It keeps doing X when...”. Slogan: Privilege the process.

She suggests teaching these three ways of thinking, and using them to guide (and interpret the results of) the “What do we notice?” and “What would you like to know?” questions that we so often use in solving a problem. The ways of thinking are rooted in what we observe — about both the problem and our way of responding to it — and so our discussions in class should bring out those observations and connect them to the thinking we’d like to impart to our students.

Steve Leinwand

Engaging, high-energy talk. The slides (pptx) are available on his web site. Main take-aways:

• In contrast to the previous speaker, he contends SMPs #1-4 are the important parts — especially #3, about constructing and critiquing arguments.
• We absolutely must observe and coach each other, and assess how many of the NCTM’s Mathematical Teaching Practices we are meeting in class.
• “It is unreasonable and unprofessional to expect professionals to change by more than 10% a year.” But...
• “It is unreasonable and unprofessional for us to be changing by much less than 10% a year.” (10% being about 6-10 min per class, or 18 days a year, or 1 unit a year.)
• Frequent cumulative review is essential for retention.
• Exit slips are essential for assessing progress and guiding next day’s instruciton.
• A “2-4-2” model of HW: Two (or maybe three) problems on a new skill, four cumulative-review problems (one each from past day, week, and month, plus one more), and two that require showing work or explanation — mathematical reasoning and justification for that reasoning.
• Questioning: Work on increasing the DoK (depth of knowledge) elicited. Handy reminder posters: “Why?” “How do you know?” “Convince us!” “Please explain.” “Draw a picture.” These are reminders for the teacher, not the students!
• Problems: Don’t state a question. Give a situation, and ask the students for questions.
• Crucial actions: struggle, explore, share, justify, compare, debrief, and consolidate.
• The teacher is most useful for organizing and consolidating knowledge at the end — not for presenting it at the beginning.

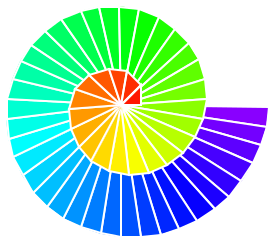
The logo

One last item: I liked this year’s conference logo — based on the Spiral of Theodorus — and felt compelled to figure out how to code it up myself between talks:

I couldn’t get the color gradient quite right: where mine passes through light green and cyan, the actual conference logo passes through dark green and violet shades. I haven’t thought much about computing color gradients, but it could make for a great project — especially considering that color schemes are modeled geometrically with each color corresponding to a point in a cube, cylinder, spiral, or other geometric object. I’ll have to keep that in mind for the computational geometry course I hope to eventually get to teach.

The other neat thing about writing code to generate the picture is that now I can see what more extreme cases look like — say, with about a thousand triangles: