As before, I’m concluding this year’s geometry classes with an all-too-quick look at right triangle trig and the area of regular polygons. This is a great way to wrap up the school year.

Some reasons:

• The unit previews the work the students will be doing in Alg II with the trig functions.

• It gives ample opportunity to practice using the Pythagorean Theorem and finding unknown sides in similar triangles.

• "How can we find the area of a regular N-gon?" is now a problem that the students have enough background to comprehend and (with a little help) answer successfully. It’s also not terribly hard to sell as a reasonable question.

• The problem has a nice conclusion when the students see the connection to pi and realize that the regular polygons become more circular as N grows.

• The pi observation serves as a preview of limits for those students going on to pre-calculus.

Also, the students are pretty uneven in their ability to handle the algebra of proportional reasoning— especially where compound expressions are involved— so this gives me opportunities to correct misconceptions and reinforce prior learning from algebra.

Two big questions

The most important questions here are:

• How can we find the area of a regular N-gon?

• How can we represent direction?

I’ve already talked a bit about the first, but the second deserves attention as well. A recurring question in my class this year has been "How can we assign a number to x?", where x progresses from length and angle and direction to 2-D size and shape. Measurement is a unifying idea that I’d like to see us push down into the lower grades in these same terms. Somewhere in the process of learning algebra, a lot of the students lose sight of this big-picture goal; I often ask a question like, "What does 20 mean, geometrically, in this problem?" and get a response like, "20 is 2x." This is pretty typical of the fuzzy thinking (or non-noticing) that I’m always trying to bring to the students’ attention. Explicitly and repeatedly making the connection between the numbers and reality helps keep them aware of why we’re doing the math.

Anyway, back to right triangles. The big opportunity they present is connecting the two major representations of direction: slope and angle. The game Gimme Friction (warning: it’s a page with sound) is great for presenting that idea. Play with it for a minute, and you’ll see both of the two representations at work.

How can we represent the gun’s direction? The gun swings back and forth; it oscillates between directly rightwards and directly leftwards, and the best representation of this is an angle that oscillates between zero and 180 degrees.

How about the ball’s direction? A ball in motion appears at first glance to have only one characteristic that changes: its location. We know from Algebra I that this consists of an x- and a y-coordinate. But if we want to make the ball move onscreen, we have to adjust those coordinates over time. There isn’t (for the students, at least) any obvious way to get from the ball’s angle of motion to its new coordinates; it’s far simpler to give the ball a second characteristic, velocity, and represent that as an (x,y) pair— or, more accurately, a (dx,dy) pair— as well. This still contains enough information to know the ball’s direction via its other form, slope: the ratio of dx to dy. And for our game programmer, this gives a trivial way to move the ball: just add dx and dy to its coordinates.

Last, we need a way to connect the two representations: at the moment the gun launches a ball, we have to convert the gun’s angle into a starting velocity. This is where the trig ratios come in; if we know how fast we want the ball to be moving along its line (say, in pixels per clock tick), we can figure out the x and y components of its velocity with sin and cos.

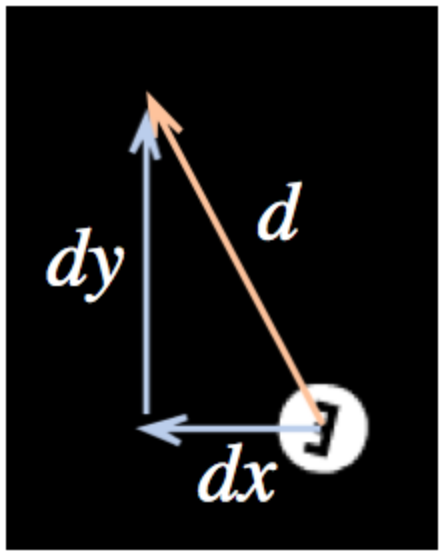
This is one reason I’d like to get the students doing some programming before reaching this point; for anybody who’s making a game like this, such problems are pretty compelling (and satisfying to solve, especially when you can produce a working game as an end result).

Exercise for more advanced readers: how can we compute which way the ball should bounce, when it hits another ball?